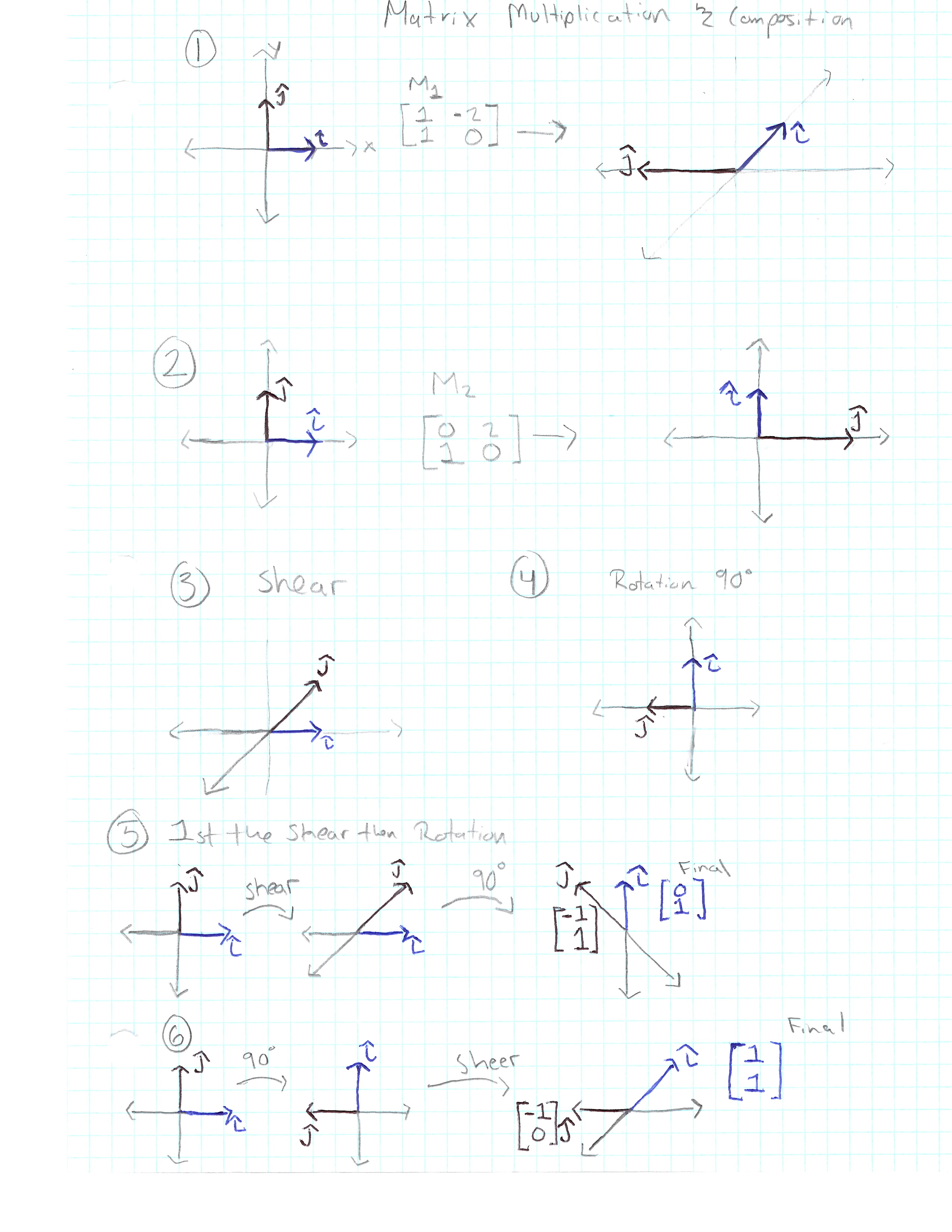
Matrix Multiplication as Composition

Running Multiple Transformations

Often you find yourself wanting to apply one transformation after another.

For Example:

• If you first apply a rotation of the original matrix by 90 degrees.
• Then you apply a shear.

The overall effect from start to finish is a linear transformation of its own. This transformation is distinct from each transformation which it consists of. The new, resulting transformation is commonly called a composition of the two separate transformations we apply. In this case it would be a composition of a rotation and a shear.

The Composition of Two Separate Transformations

Like any linear transformation, the composition of the two separate transformation can be described all on its own, by simply following i and j. Let us consider the following after the composition of a rotation and a shear.

i -> [ 1 ]   and   j -> [-1 ]
     [ 1 ]              [ 0 ]   

Which results in the following matrix:

[ 1 -1 ]
[ 1  0 ]

This new matrix captures the overall effect of a rotation, then a shear, but as one single action rather than two successive ones. Let us consider a vector v, we can first multiply v by the rotation matrix. Then we would multiply the result by the shear matrix. The individual transformations are the same as applying the composition matrix to v.

[ 1  1 ]( [ 0 -1 ][ x ] )   =   [ 1 -1 ][ x ]
[ 0  1 ]( [ 1  0 ][ y ] )       [ 1  0 ][ y ]
  ^  ^      ^  ^                  ^  ^
(Shear)  (Rotation)            (Composition)

Let’s take a look at the computation which explains this behavior.

The Product of Two Matrices

Based on the notation, it is safe to say, that the composition matrix is the product of the original two matrices. Always remember, when multiplying two matrices like this, it has the geometric meaning, of applying one transformation, then another. Also keep in mind, that you read the following from right to left. You first apply the transformation of the matrix to the right (rotation), then the transformation of the matrix on the left (shear). This steams from function notation f(g(x)).

      f( g(x) )
<--------------
[ 1  1 ][ 0 -1 ]   =   [ 1 -1 ]
[ 0  1 ][ 1  0 ]       [ 1  0 ]
  ^  ^    ^  ^           ^  ^
(Shear)  (Rotation)    (Composition)

Example of Matrix Multiplication

Let’s look at the following example. We have a Matrix M1 and a matrix M2. (Pictures 1 and 2 below).

  M2      M1
[ 0  2 ][ 1 -2 ]    =   [ ?  ? ]
[ 1  0 ][ 1  0 ]        [ ?  ? ]

Let’s see if we can figure out the resulting matrix without drawing it out.

1. We need to figure out where i goes.
   1. We must apply the first change which happens in i of M1, by multiplying M2 by i of M1.

   2. This will give us the i of the composition Matrix.

        M2      M1
      [ 0  2 ][ 1 -2 ]    =   [ ?  ? ]
      [ 1  0 ][ 1  0 ]        [ ?  ? ]
      
      [ 0  2 ][ 1 ]    =   1[ 0 ]  +  1[ 2 ]    =    [ 2 ]  
      [ 1  0 ][ 1 ]         [ 1 ]      [ 0 ]         [ 1 ]
      
        M2      M1
      [ 0  2 ][ 1 -2 ]    =   [ 2  ? ]
      [ 1  0 ][ 1  0 ]        [ 1  ? ]
      

2. We need to figure out where j goes.
   1. We must apply the second change which happens in j of M1, by multiplying M2 by j of M1.

   2. This will give us the j of the composition Matrix.

        M2      M1
      [ 0  2 ][ 1 -2 ]    =   [ 2  ? ]
      [ 1  0 ][ 1  0 ]        [ 1  ? ]
      
      [ 0  2 ][-2 ]    =  -2[ 0 ]  +  0[ 2 ]    =    [ 0 ]  
      [ 1  0 ][ 0 ]         [ 1 ]      [ 0 ]         [-2 ]
      
        M2      M1
      [ 0  2 ][ 1 -2 ]    =   [ 2  0 ]
      [ 1  0 ][ 1  0 ]        [ 1 -2 ]
      

Final Equation

1. Initially, i will always land on the first column of the right matrix (M1).

   1. Therefore, by multiplying the first column of the right matrix (M1) by the left matrix (M2), the product will give i’s’ final location, and be the first column of the composition matrix.

        M2      M1
      [ a  b ][ e  f ]    =   [ ?  ? ]
      [ c  d ][ g  h ]        [ ?  ? ]
      
      [ a  b ][ e ]  =  e[ a ]  +  g[ b ]  =  [ ae + bg ]
      [ c  d ][ g ]      [ c ]      [ d ]     [ ac + dg ]
      
        M2      M1
      [ a  b ][ e  f ]    =   [ ae + bg   ? ]
      [ c  d ][ g  h ]        [ ce + dg   ? ]
      

2. Initially, j will always land on the second column of the right matrix (M1).

   1. Therefore, by multiplying the second column of the right matrix (M1) by the left matrix (M2), the product will give j’s final location, and be the second column of the composition matrix.

        M2      M1
      [ a  b ][ e  f ]    =   [ ae + bg   ? ]
      [ c  d ][ g  h ]        [ ce + dg   ? ]
      
      [ a  b ][ f ]  =  f[ a ]  +  h[ b ]  =  [ af + bh ]  
      [ c  d ][ h ]      [ c ]      [ d ]     [ cf + dh ]
      
        M2      M1
      [ a  b ][ e  f ]    =   [ ae + bg    af + bh ]
      [ c  d ][ g  h ]        [ ce + dg    cf + dh ]
      

The Concept over the Equation

It is common to be taught a formula and algorithmically approach the product.

[-3  1 ][ 5  3 ]  =  [(-3)( 5) + ( 1)( 7)  (-3)( 3) + ( 1)(-3)]
[ 2  5 ][ 7 -3 ]  =  [( 2)( 5) + ( 5)( 7)  ( 2)( 3) + ( 5)(-3)]

But what’s more important is understanding what matrix multiplication represents. Which is applying one transformation after another.

Question: Does it matter which matrix is on the right?

    ???
M1M2 = M2M1

Let’s take the earlier composition, which consists of the following two transformations.

1. A shear, which fixes i but squishes j over to the right. (Picture 3 below)
2. A 90-degree rotation, counterclockwise (Picture 4 Below).

If we first do the shear then rotation, we see the following: (Picture 5 Below)

i -> [-1 ]   and   j -> [ 0 ]
     [ 1 ]              [ 1 ]   

If we first do the rotation then the shear, we see the following: (Picture 6 Below)

i -> [ 1 ]   and   j -> [-1 ]
     [ 1 ]              [ 0 ]   

Therefore we can conclude the following:

M1M2 != M2M1

This conclusion makes it very important to remember to read matrix multiplication from right to left.

Is Matrix Multiplication Associative?

    ???
(AB)C = A(BC)

Instead of drawing out 3 matrices and mindlessly multiplying them. Let us consider each letter as a matrix and follow the transformations, using the principle we learned earlier. Me must multiply everything from right to left.

Therefore we can see that (AB)C means that we do the following transformations:

1. We transform by matrix C.
2. Then we transform by matrix B.
3. Finally we transform by matrix A.

Now if we take a look at A(BC) and follow the transformation:

1. We transform by matrix C.
2. Then we transform by matrix B.
3. Finally we transform by matrix A.

The essence of this being that, instead of multiplying 3 matrices, we should consider what each matrix multiplication implies; It implies one transformation after another (starting from the right).

The key takeaway is that instead of multiplying matrices numerically, we must always consider the individual transformations behind the multiplication. This will allow us to practice the concept and visualize the composition, instead of having a strict algorithmic approach that provides us with no real insight.