Inverse Matrices, Column Space and Null Space

As you might be able to tell, a bulk what we have done so far is about understanding Linear algebra from the visual lens of linear transformations. This topic will be no different, we will take a look at inverse_matrices, column space, rank and null space.

Fair warning, we won’t be going over computation though. Perhaps in a later topic or edit, I will go over computation using “Gaussian elimination” and “Row echelon form”. But the truth is that there are many tools that we can leverage to do the complex computation for us. As the common theme in many of these posts, I will be focusing more on the concepts over the computation.

As of now we have a good understanding of where linear algebra can be applied. The manipulation of space can be useful in fields like computer graphics and robotics. But one of the main reasons it is taught to students of far spending disciplines is because it allows us to solve certain systems of equations.

Linear Systems of Equations

What I mean by system of equations is having a list of unknown variables, and a list of equations relating them.

            6x - 3y + 2z = 7
x y x        x + 2y + 5z = 0
^ ^ ^       2x - 8y -  z =-2
Unknown      ^    ^    ^   ^
Variables       Equations

In a lot of cases these equations can get complicated, but if you’re lucky, they might take a certain special form. Within each equation, the only thing happening to each variable is that it is being scaled by some constant, and the only thing happening to these scaled variables is that they’re added to each other.

Meaning that we won’t have any exponents (x^2), fancy functions (sin(x)), or two variables being multiplied by each other (xy).

The typical way to organize these special systems of equations is to throw all the variables to the left and all the constants to the right. It’s also smart to line up all the variables and throw in any zero’s if the variable doesn’t show up in one of the equations. This is called a linear system of equations.

            2x + 5y + 3z =-3
            4x + 0y + 8z = 0
            1x + 3y + 0z = 2

You might notice that this looks a lot like matrix-vector multiplication. We can package all these equations together into a single vector equation. The matrix will contain all of the constant coefficients (A), the vector will contain all of the variables (x), and their matrix-vector product will equal some different constant vector (v).

                              Variables
                                 ˅
2x + 5y + 3z =-3    [ 2  5  3 ][ x ]   [-3 ]
4x + 0y + 8z = 0 -->[ 4  0  8 ][ y ] = [ 0 ]
1x + 3y + 0z = 2    [ 1  3  0 ][ z ]   [ 2 ]
                      ^  ^  ^            ^
                      Constant        Constants
                      Variables
                      ^  ^  ^    ^       ^
                            A    x       v

This is more than some trick on setting up our equation, it sheds light on a cool geometric interpretation for the problem. The matrix A corresponds to some linear transformation. Therefore solving Ax = v means we are looking for some vector x, which after the transformation, lands on v.

We can think about the system of equations representing an unknown vector, which after a given transformation provides us with its final location.

Let’s start by looking at a simple system of equations by having only two equations and two unknowns. Meaning that A is a 2 x 2 matrix, and both x and v are two-dimensional vectors.

2x + 2y =-3
1x + 3y =-1

[ 2  2 ][ x ] = [-4 ]
[ 1  3 ][ y ]   [-1 ]

The way we start thinking about a solution to this equation whether the transformation associated with A squishes all of space into a lower dimension or leaves everything the two dimensions.

In the language of our last topic, we can divide the cases into ones where A has a zero determinant or a non-zero determinant.

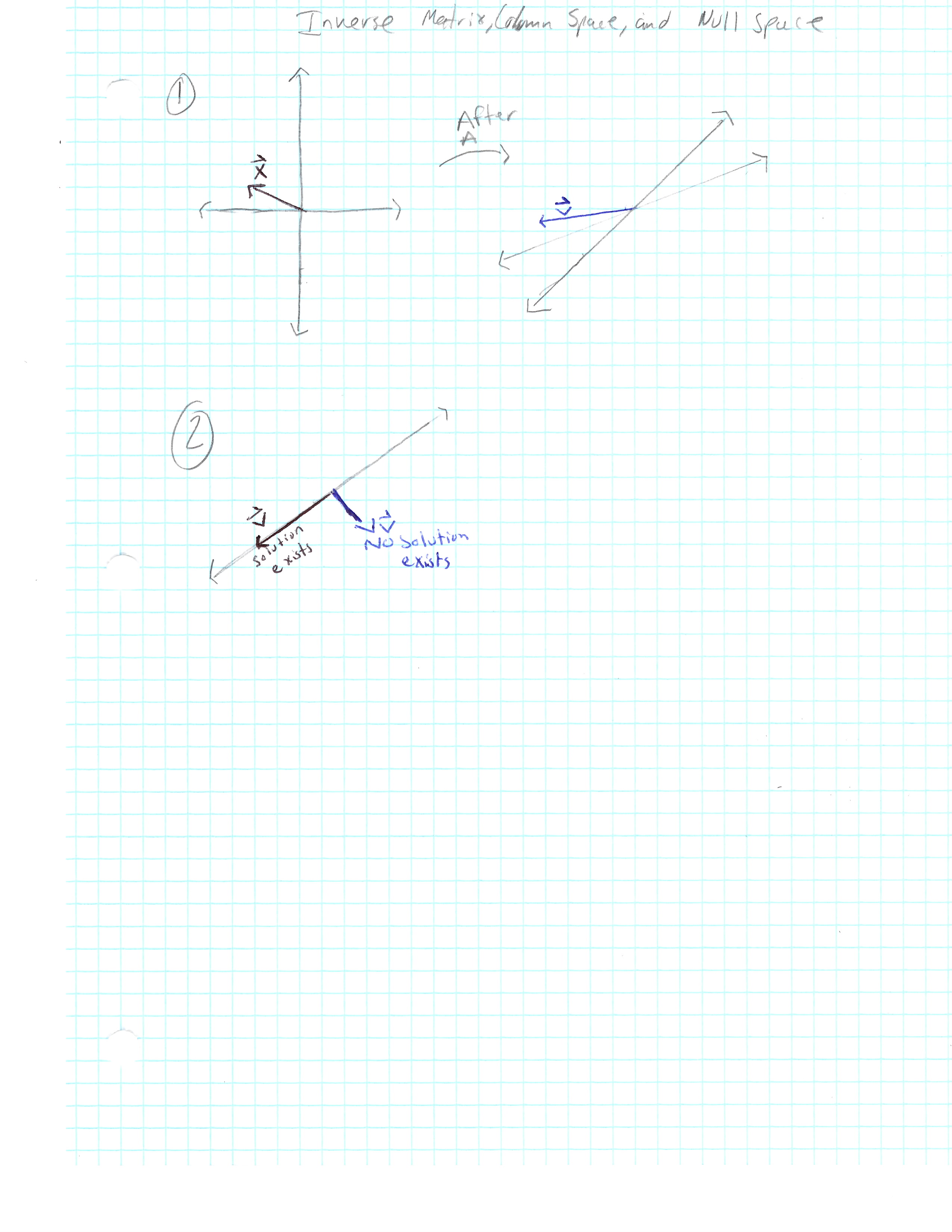
Let’s look at the more common case where A does not get squished into a lower dimension. In this case, there can only be one vector that lands on v after the transformation. We can find this vector by playing the transformation in reverse (see picture one).

Inverse Transformation

When we play the transformation in reverse it corresponds to a separate linear transformation commonly called, the inverse of A which is denoted as A^-1.

For Example, if A was a counterclockwise rotation by 90 degrees, then the inverse of A would be a clockwise rotation by 90 degrees. The inverse of A would bring it back to its original start position.

A = [ 0 -1 ]
    [ 1  0 ]

A^-1 = [ 0  1 ]
       [-1  0 ]

In general, A inverse is the unique transformation with the property that if you first apply A then follow it with the transformation A inverse, you end up where you started (Remember that we multiply matrices from right to left).

    Transformation
         ˅
  A^-1 * A    = [ 1  0 ]  < Transformation that
  ^^^           [ 0  1 ]  < does nothing
  Inverse
  Transformation

Multiplying A by A^-1 can be captured by matrix multiplication. So that the core property of the transformation A inverse times A equals to the matrix which corresponds to doing nothing. The transformation that does nothing is called the identity transformation. The identity transformation leaves i and j each where they are, unmoved.

Once you find this inverse, which is usually done using a computer, you can solve your equation by multiplying this inverse matrix by v.

       Ax = v
A^-1 * Ax = A^-1 * v
^^^^^^^^
The "do nothing" matrix

        x = A^-1 * v

What this means geometrically is that you are transformation in reverse and following v to see where it started. This Non-zero case determinant case which is by far more common, tells us that if you have two unknowns and two equations, that the is more almost certainly a unique solution.

ax + cy = e
bx + dy = f

This idea is also present in higher dimensions when the number of equations is equal to the number of unknowns. Reiterating the idea that you apply some transformation A to vector x, and get the resulting vector v. As long as the transformation A doesn’t squish all of space into a lower dimension (have a nonzero determinant), there will exist a transformation A^-1 where if you first do transformation A then A^-1, it is the same as doing nothing. And to solve your equation, you simply have to multiply that inverse transformation, A^-1, by v.

              Ax = v

2x + 5y + 3z =-3    [ 2  5  3 ][ x ]   [-3 ]
4x + 0y + 8z = 0 -->[ 4  0  8 ][ y ] = [ 0 ]
1x + 3y + 0z = 2    [ 1  3  0 ][ z ]   [ 2 ]

The Uncommon Case

But when the determinant of the transformation is zero, and it squishes all of the space into a smaller dimension, there is no inverse. You cannot unsquish a line and turn it into a plane, no function is capable of doing that.

Similarly in three dimensions, if transformation A squishes the plane into two dimensions, a line, or a point, there is no way to get its inverse. Those all result in a zero determinant.

It is still possible to get a solution if your determinant is zero, you just have to be lucky enough that your resulting vector v lives somewhere on that line (see picture two).

You might notice that some squishes feel more restrictive than others. For example, in three dimensions, it seems far more unlikely to find a solution when the plane is squished onto a line, versus when it is squished onto a plane. Keeping in mind that both of those squishes have a zero determinant.

We have some language that explains this concept instead of calling it a zero determinant. When the output is a line, meaning that it is one-dimensional, it has a rank of one. If all the vectors land on some two-dimensional plane, then we say that it has a rank of two. The word rank corresponds to the number of dimensions in the output of the transformation.

For instance, in a 2 x 2 matrix, rank two is the best rank that it can have since the basis vectors continue to span the full two dimensions of space and have a nonzero determinant. But if we have a 3 x 3 matrix, rank two means that we have collapsed into a smaller dimension. But not as much as we would have if the resulting transformation was a rank one. If a three-dimensional transformation has a non-zero determinant and its output fills all of three-dimensional space, then it has a rank of three.

Column Space

This set of all possible outputs for your matrix, whether it’s a line, a plane, or a three-dimensional space, it is called the column space of your matrix.

The name comes from the columns of your matrix, which tell you where your basis vectors land, and the span of those basis vectors gives you all possible outputs. In other words, the column space is the span of the columns in your matrix.

Therefore a more accurate definition of rank is that it’s the number of dimensions in the column space. When the rank is as high as it can be, meaning that it equals the number of columns, we call the matrix full rank.

Null space

Keep in mind that the zero vector will always be included in the column space, [ 0, 0], since linear transformations must keep the origin fixed in place. For full rank transformations, only vector [0, 0] lands on the origin. But for transformations which are not full rank, you can have a bunch of vectors that land on zero.

If a two-dimensional transformation squishes the plane onto a line, there is a separate line full of vectors which get squished onto the origin. If a three-dimensional transformation squishes everything onto a plane, there is also a line full of vectors which land on the origin. If a three-dimensional transformation squishes everything onto a a line, there is a whole plane full of vectors which land onto the origin.

This set of vectors which land on the origin is called the null space or the kernel of your matrix. Its the space of all vectors which become null, since they land on the origin, [0, 0].

In terms of linear systems of equations, if v happens to land on the kernel, the null space gives you all possible solutions to the equation.

Conclusion

That is a very high-level overview of how to think about linear systems of equations geometrically. Each system has some sort of linear transformation associated with it. If that transformation has an inverse, it can be used to solve your system. Otherwise, the idea of column space lets us know when a solution even exists. The idea of a null space helps us to understand what the set of all possible solutions can look like.

There is a lot that wasn’t covered here. We didn’t go over the computation of these systems. We also only looked at linear systems of equations, where the number of unknowns equals the number of equations. But the point of this topic was to understand the concepts behind inverse matrices, column space and null space. Having a strong grasp on these concepts will make any future learning more fruitful.