The Determinant

Scaling a Region

So far within our transformation, you might have noticed that some transformations stretch the plane while others squish it. It might be useful to know exactly how much things are being stretched or squished. More specifically to measure the factor of which a given area or region increases or decreases.

Simple Transformation

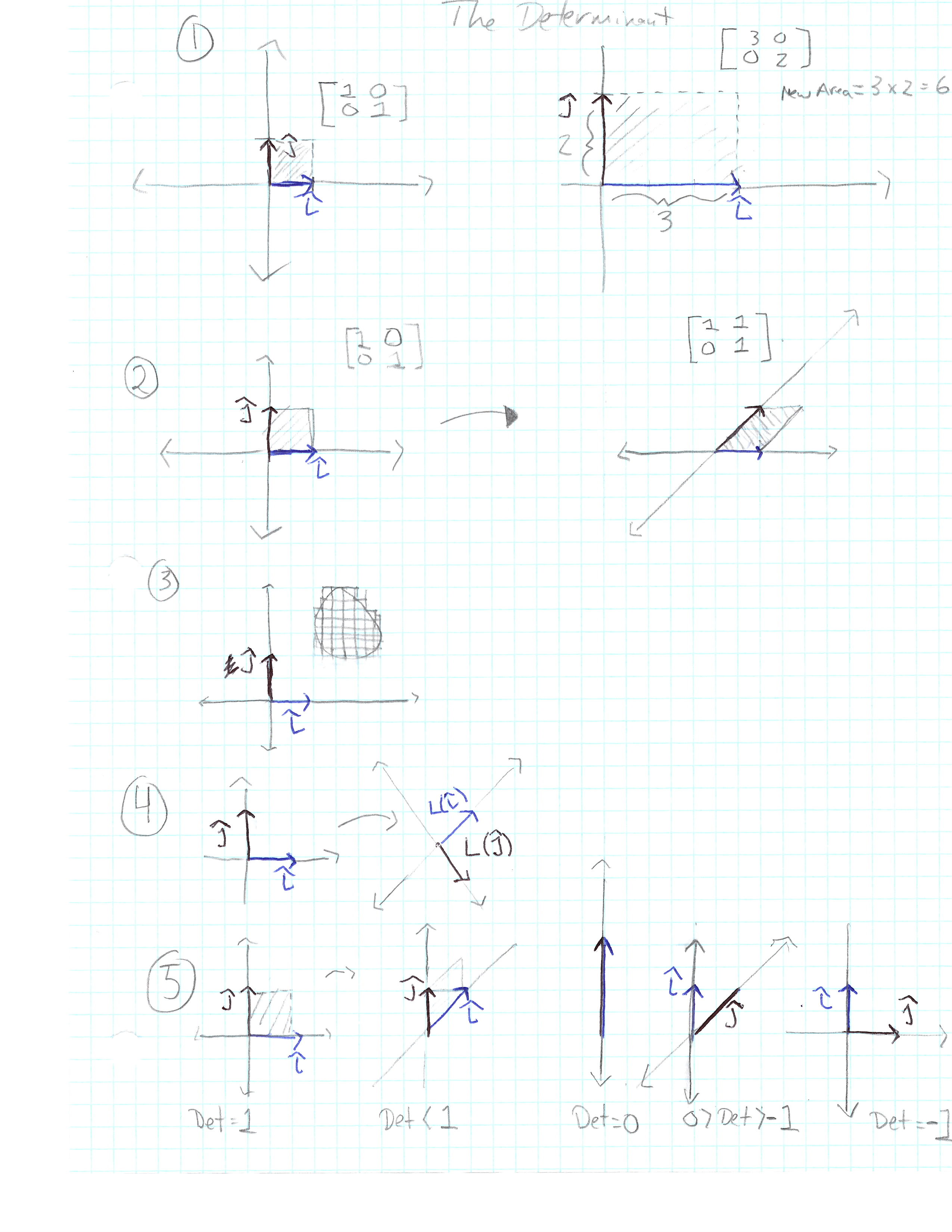
For example, let’s take a look at the following matrix and draw it out (see picture one).

[ 3  0 ]
[ 0  2 ]

If we focus our attention on the 1 x 1 square in the original matrix, whose bottom sits on i and left side sits on j. After the transformation occurs, the square transforms into a 3 x 2 rectangle.

Since it started with an area of 1 and ended with an area of 6, we can say that after the transformation, the area was scaled by a factor of 6.

A Shear

Now let’s take a look at a shear instead and draw it out (see picture two).

[ 1  1 ]
[ 0  1 ]

The same 1 x 1 square gets slanted and turned into a parallelogram. But the area of the parallelogram is still 1, since the base and height of the parallelogram as 1 x 1. Although this transformation squishes the plane, it leaves the area the same, as least for that one square.

Rule of Thumb

If you can tell how much the area of that 1 x 1 changes, it can tell you any possible region of space changes, due to the transformation. Whatever happens to one square in the grid, has to happen to all the square in the grid, no matter the size. This is due to the earlier rule we have, all grid lines must remain parallel and evenly spaced.

Area of a Shaped Curve

If we have a shape that is not a grid square, it can be approximated by grid squares pretty well. Depending on the size of the grid squares we put inside the shaped (see picture 3).

So if the area of all those tiny grid squares is being scaled, the area of the entire shape will also be scaled by that same amount.

The Determinant

The value which we use to describe the scaling of the 1 x 1 square, is known as the determinant of that transformation. We will go over how to numerically compute the determinant later on, but understanding what it represents is far more important.

The determinant of a transformation would be 3 if that transformation increases the area by a factor of three.

det([ 0.0  2.0 ]) = 3
   ([-1.5  1.0 ])

The determinant of a transformation would be 1/2 if that transformation squishes the area by of all squares by a factor of 1/2.

det([ 0.5  0.5 ]) = 0.5
   ([-0.5  0.5 ])

The determinant of a two-dimensional transformation is 0, if it squishes all of space onto a line, or onto a single point. Since then, the area of any region would become 0.

det([ 4  2 ]) = 0
   ([ 2  1 ])

The realization of this is very important. It means that checking to see if the determinant of a given matrix is 0, will tell us whether or not the transformation associated with that matrix squishes everything into a smaller dimension. Or in some extreme cases, is on a single point.

det([ 0  0 ]) = 0
   ([ 0  0 ])

Maybe I Didn’t Tell You Everything…

It is possible of having a transformation with a negative determinant. But what does a negative determinant even tell us?

det([ 1  2 ]) = -2.0
   ([ 3  4 ])

This has to do with the idea of orientation. There are transformation that seems to flip over the plane. If we think about a piece of paper, they seem to flip the page over onto the other side. Any transformation that does this, is said to invert the orientation of space.

Another way to think about it is with i and j. Notice that in their starting position, j is to the left of i. If after a transformation, j is on the right of i, the orientation of space has been inverted (see picture 4).

Whenever this happens, whenever the orientation of space is inverted, the orientation will be negative. The absolute value of the determinant will still tell you the factor by which areas have been scaled.

det([ 2  1 ]) = -5.0
   ([-1 -3 ])

Why Does Negative Mean Orientation-Flipping?

So the question arises, why would orientation-flipping be naturally described by a negative determinant? The closer i gets to j the more the determinant decreases. Eventually as i and j “touch”, the determinant is 0. Now that j is to the right of i and they are moving apart, doesn’t it make sense to describe the value as a negative (see picture 5)?

Determinants in Three Dimensions

Like with Two-Dimensions, the determinant tells you how much a transformation scales things. But now instead of telling you the area that is scaled, it tells you how to scale the volume.

Just as in two-dimensions we follow the area of the 1 x 1 square during a transformation. In three-dimensions it’s best to follow the volume of the 1 x 1 x 1 cube during a transformation. The resulting slanty cube is called a “Parallelepiped” (try saying that 5 times really fast).

det([ 1.0  0.0  0.5 ]) = Volume of the
   ([ 0.5  1.0  0.0 ])   resulting
   ([ 1.0  0.0  1.0 ])   parallelepiped

As we said earlier, if we have a determinant of 0 it has one of two meanings. Either the three-dimensional plane has been squished down a dimension. Meaning that it is now on a flat plane (two-dimension), a line (one-dimension), or in extreme cases, onto a single point.

Those of you who read the second post will recognize that the columns of the matrix are linearly dependent.

det([ 1.0  0.0  0.5 ]) = 0
   ([ 0.5  1.0  0.0 ])   
   ([ 1.0  0.0  1.0 ])   
       ^    ^    ^
     Columns must be
     linearly dependent

Negative Determinants in Three-Dimensions

The easiest way to tell if the determinant is positive is to use the right-hand rule (Consider a to be i, b to be j and a x b to be k).

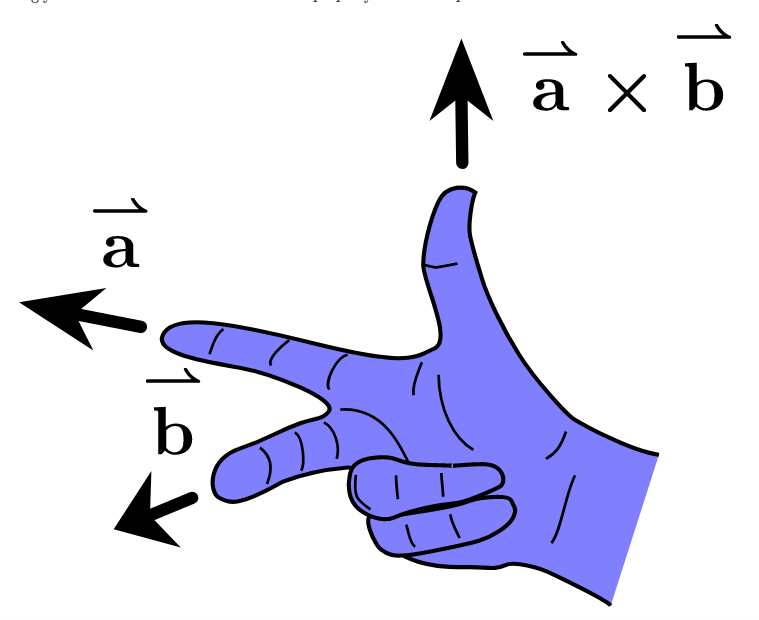
If after the transformation you can still use the right-hand rule, then orientation has not changed, and the determinant is still positive. Otherwise, if it makes more sense to use your left hand to describe the matrix, orientation has been flipped, and the determinant is negative.

Computing the Determinant

The formula for two-dimensions is:

det([ a  b ]) = ad - bc
   ([ c  d ])

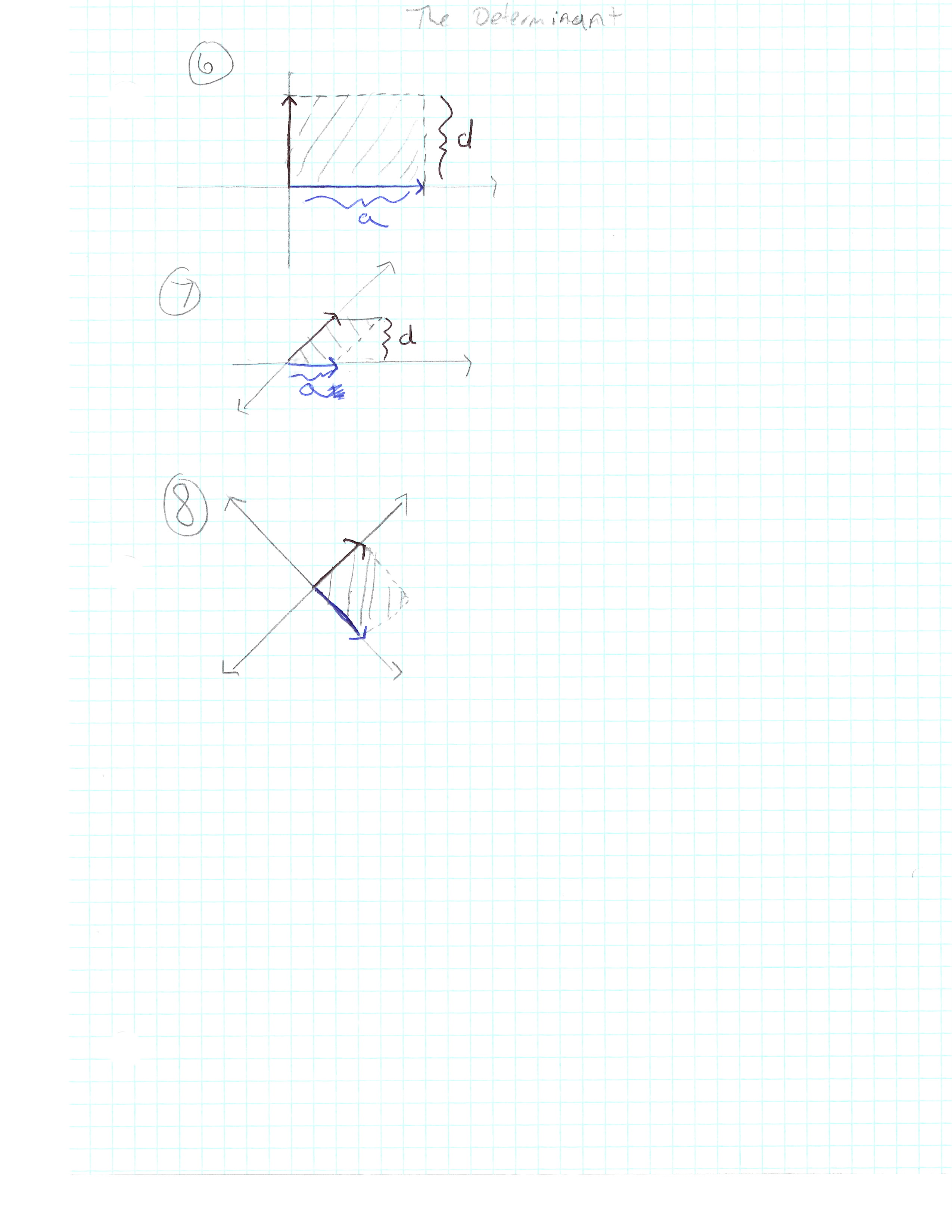
Let’s take a look at how this formula came to be. If we make b, c = 0, a tells you how much i is stretched in the x direction and d tells you how much j is stretched in the y direction (see picture six).

det([ a  0 ]) = ad - 0 * 0
   ([ 0  d ])

This makes sense, since a * d gives us the area of the rectangle that our 1 x 1 unit square turns into. This is evident if we look at our earlier example (see picture one).

[ 3  0 ]
[ 0  2 ]

Even if one of b or c is 0, we get a parallelogram, with a base of a and a height of d (see picture 7).

det([ a  b ]) = ad - b * 0
   ([ 0  d ])

If both b and c are non-zero, then the b * c term, tells us how much the parallelogram is stretched or squished in the diagonal direction (see picture seven).

For those of you who want a more in-depth proof, take a look at this.

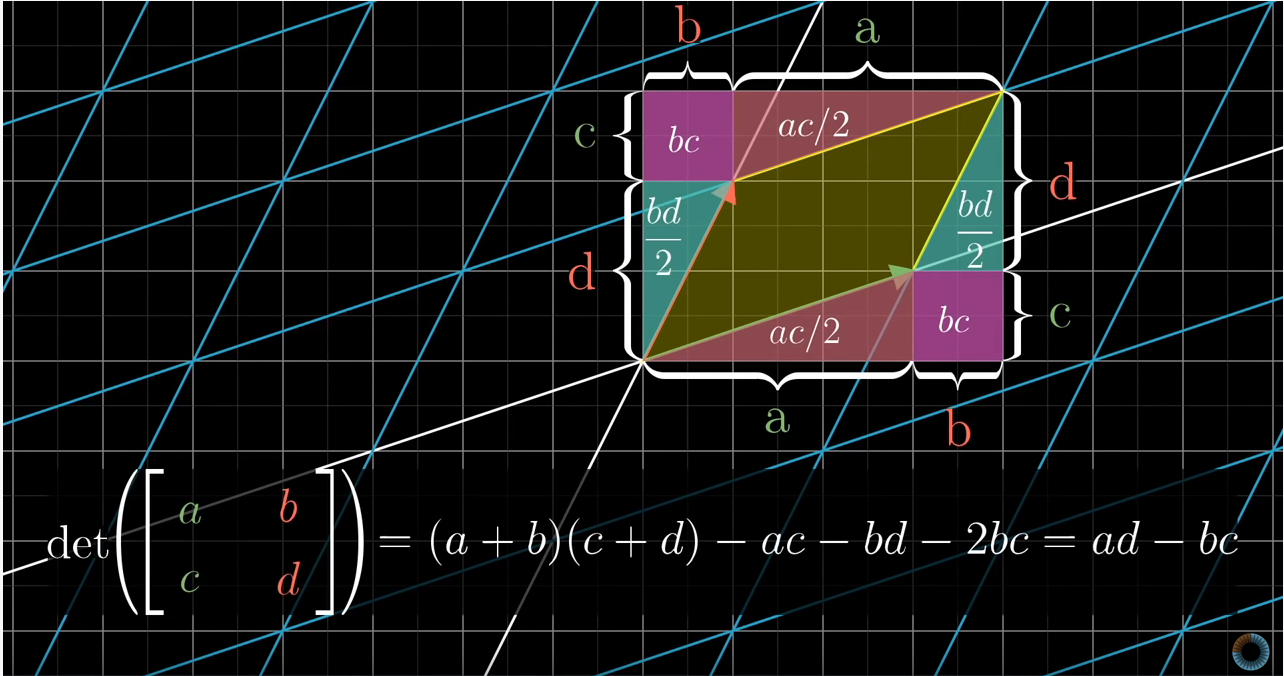
This is also true for finding the determinant in three-dimension.

det([ a  b  c ]) =
   ([ d  e  r ])
   ([ g  h  i ])
                    a det([ e  f ])
                         ([ h  i ])

                  - b det([ d  f ])
                         ([ g  i ])

                  + c det([ d  e ])
                         ([ g  h ])

Key Concept

I believe that computing the determinant is not necessarily important to understand the essence of linear algebra. While being able to understand what the determinant represents, falls within that essence.

Here’s a fun activity, try to rationalize the following in one sentence. It would take forever to do this using computation, but if you understand the key concept of the determinant, it’s fairly straight forward.

det(M1 * M2) = det(M1) * det(M2)