Linear Combinations, Spans and Basic Vectors

Thinking about Vector Coordinates

Think about each coordinate as a scalar

• What effect does it have on the vector?
• Does it Squish or Stretch the vector.

  Common Vectors

• i, which is equal to one unit to the right of the X axis from the origin.
• j, which is equal to one unit going up of the Y axis from the origin.

Visualizing Vectors

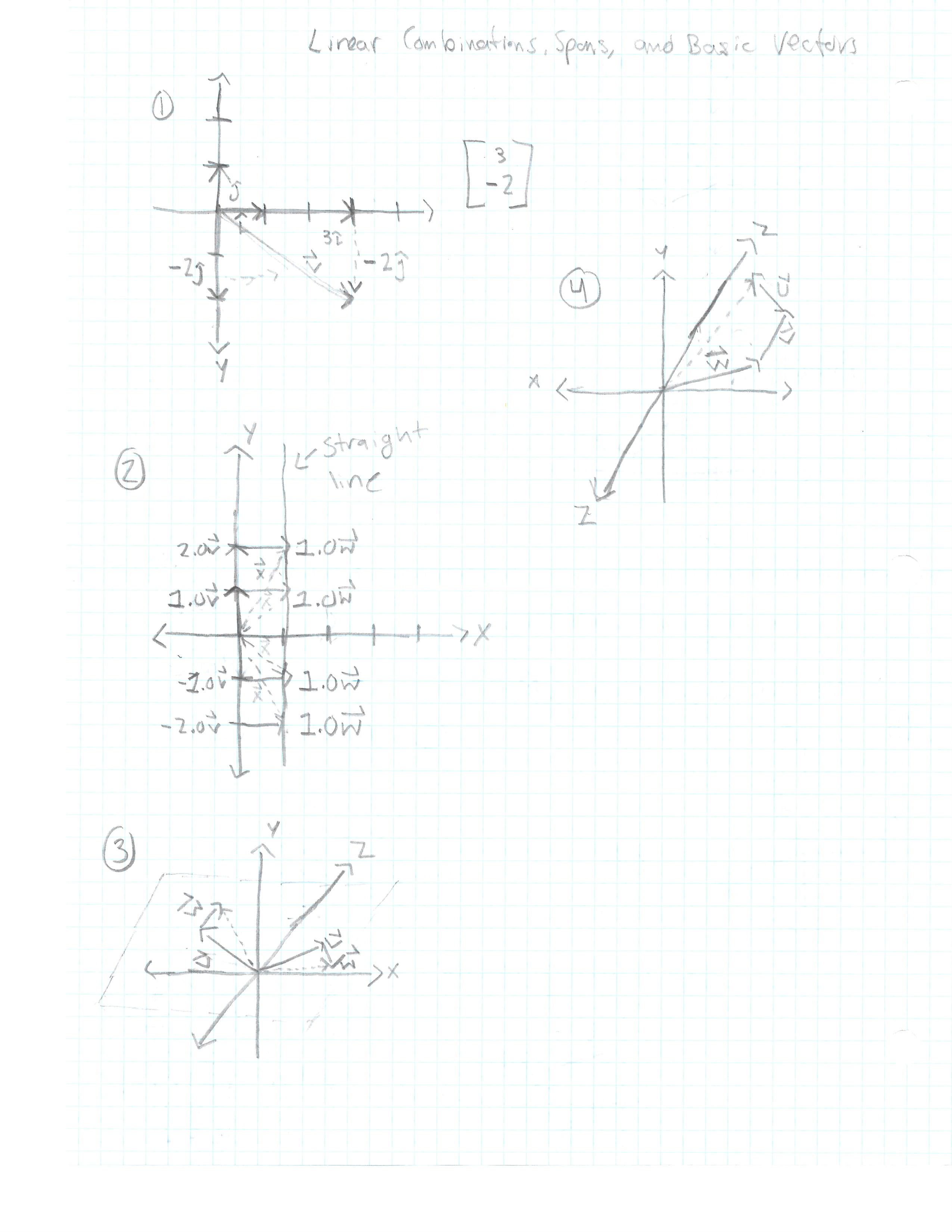
• Consider 2 vectors, 3i and -2j.
• On the X coordinate, think of 3 as a scalar, scaling i by 3.
• On the Y coordinate, think of -2 as a scalar, scaling j by -2.
• The resulting vector V is the sum of the two scaled vectors.
• This is a very important concept, adding together two scaled vectors.
• See Imagine 1 Below

Basis Vectors

i and j are considered “basis vectors”, together they are known as the “basis of a coordinate system”. When thinking about a coordinates as scalars, the basis vectors are what those scalars scale.

Consider using a different basis

• Instead of using i and j as basis vectors to describe our vector, we could use different basis vectors.
• Ultimately we could use every combination of 2 scaled basis vectors to describe a resulting vector.
• But by sticking to i and j as out basis vectors, we have an easier time visualizing.
• Anytime we describe vectors, it depends on an implicit choice of what basis vectors we are choosing.

Linear Combination

• Anytime that you are scaling two vectors and adding them together, it is called a linear combination of the two vectors.

• av + bw, where a and b are scalars.

• Consider 2 scalars, one which is fixed while the other moves freely.
  • v will move freely while w is fixed.
  • The tip of the the resulting vector draws a straight line.
  • See Image 2 below.

Span of Two Vectors

• The set of all possible vectors that you can reach with a linear combination of a pair of vectors, is the span of those two vectors.
• The span of most 2-D vectors is all vectors of 2-D space.
  • Except for when they line up, their span is the tip which sit on a certain line.
• Vector addition and multiplication are two fundamentally important operations.
  • The span is one way of asking, what are all the possible vectors we can reach, only using these two fundamental operations.

Vectors vs Points

• It can get “crowded” to think about a collection of vectors on a line.
• Even more so when you think of all the possible vectors on a Plane.
• When dealing with collection of vectors, it is common to think of them as a point on the plane.
  • Remember to envision the tail of the vector on the origin, and the tip on the point.
• If you’re thinking of every possible vector that sits on a line, you can simply think of the line itself.
• When thinking about every vector on a plane, you can simply think about all of the point where all of the tips sit.

Rule of Thumb:

• If you’re thinking about a single vector, think of it an arrow.
• If you’re thinking about a collection of vectors, think of them as points.

With the span example:

• The span of most 2-D vectors is all points on the plane.
• If the 2 vectors line up, their span is simple a line.

Span in 3D

Two Vectors in 3-D

• Consider two vectors in 3-D space which are not pointing in the same direction.
  • Their span is the collection of all possible linear combination of those 2 vectors.
  • All combinations that you get, when scaling the 2 vectors, and adding them in some way.
  • The tip of the resulting vector will be the equivalent of a flat sheet cutting through the origin.
  • The set of all possible resulting vectors whose tips sit on the sheet is the span of your 2 vectors.
  • See Imagine 3 below.

Three Vectors in 3-D

• Consider three vectors in 3-D space.
  • The linear combination of three vectors is described pretty much in the same was as two vectors.
  • av + bw + cu where a, b, c are the scalars.
  • You will scale all 3 vectors and add them all together.(Image 4)
  • The span of these three vectors is the set all possible linear combinations.

  Linear conbination of v, w, and u

  av + bw + cu

  For span, let constant (a, b, c) vary.

Back to the Sheet

Two things can happen here.

1. If your third vector happens to be sitting on the span of the first two vectors, nothing changes.
   1. It sits on that sheet and does not affect the span.
2. If your third vector happens NOT be sitting on the span of the first two vector, it unlocks access to every possible 3-D vector.
   1. As you scale that 3rd vector, it moves around that span sheet of the first two vectors.

Linearly Dependent

• When two vectors line up, one of the vectors is redundant.
• Whenever you have a vector which can be removed and have no effect on the span, the correct terminology is to say they are linearly dependent.
• One of the vectors can be expressed as the linear combination of the others. Since it is already in the span of the others.

Linearly Indendent

• When a vector adds to the span, it is said to be linearly Independent.

Quiz

“The basis of a vector space is a set of linearly independent vectors that span the full space.”

Consider why this definition makes sense:

Our basis consists of two vectors (i and j) which are used to represent two vectors which do not overlap. Since they do not overlap they each independently contribute to the span, in 2-D allowing them to scale to all points on the plane. Since our basis independently contributes to the span, they are a set of linearly independent vectors.