Intro to Vector

3 Ideas of a vector

• Physics
  • Vectors are length and direction
  • Get exact Definition
• Mathematics
  • Vector can be anything
  • Very abstract, ignore till later
• Computer Science
  • Lists of nums
  • Dimension depends on the size of list

Visualizing Vectors on a Plane (Physics)

• Think of an arrow in a coordinate system starting at (0,0)
• Think of an X, Y plane
• Vectors will be represented from left to right in this category
• The top number in a vector represents the x plane, negative meaning to go left
• The bottom number in the vector represents the y plane, negative meaning to go down.
• In 3D, the 3rd number represents the Z access.
• Each element in a vector will be expressed as a component

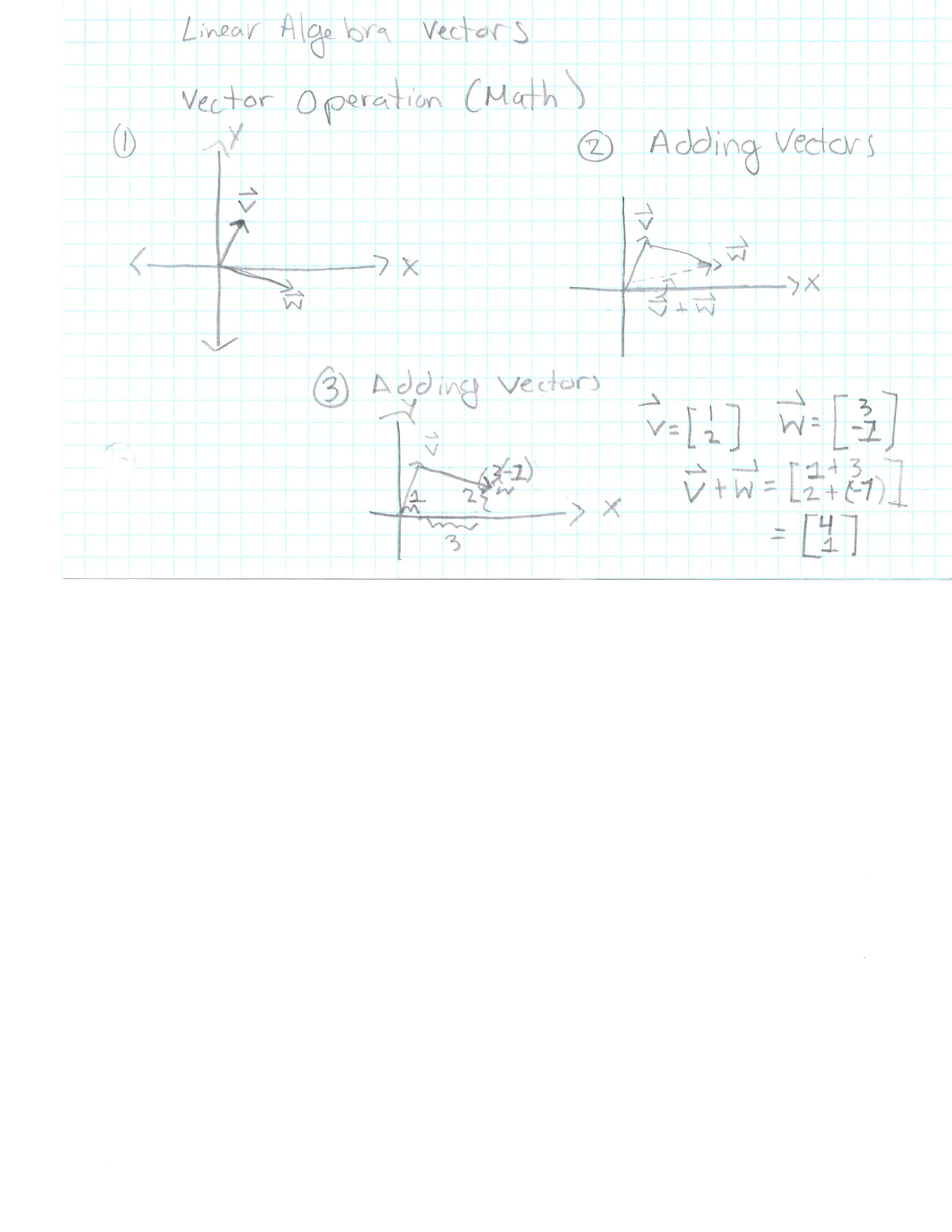
Vector Operations (Mathematic)

I will do my best to explain vector addition with words (Picture (1) below to visualize).

• Consider 2 vectors, V = [1, 2], W = [3, -1]
• Both of which start on the origin
• Tail represents where the vector starts
• Tip represents where the vector ends

  Adding Vectors

  1. Move the tail of vector W and put it at the tip of vector V (*Picture (2) below to visualize).
  2. Find the dimension of the vector from the origin to the tip of vector W
  3. Think of vectors as movement. If you move along the sum of the first vector. Then along the sum of the second vector You will get to where you are trying to go (*Picutre (3) below to visualize).
  4. Consider moving down a number line.
  1. 2 + 5
  2. First you would move 2 spaces to the right
  3. Next you would move 5 space, which would get you to 7 (Right?)
     1. Lets add the vector coordinates.
  4. Following the number line example, we can simply move according to each coordinate
     1. 1 + 3 to the right = 4
     2. 2 +(-1) to the up(?) = 1
     3. The new coordinate is [4, 1]
  5. In general, vector addition consists of adding the x coordinates and the Y coordinates.
     1. [x1, y1] + [x2, y2] = [x1+x2, y1+y2]

Multiplication of Vectors

• Let us consider vector V [3, 1]
  1. If we were to multiply vector V by 2, it is the same “stretching” the vector by twice its length.
  2. If we were to multiply vector V by 1/3, it is the same squishing the vector until its 1/3 the size.
  3. If we were to multiply vector V by -1.8, we would first flip the vector in the opposite direction. Then we would “stretch” it out 1.8x of its length.
• Scaling: Stretching, squishing, or reversing a vector is known as scaling.
  • Scalor: The multiple which is used to scale the vector. (2, 1/3, -1.8)

1. “Streching” out a vector by 2, consists of multiplying each of its components by 2.
   1. 2V = [32, 12] = [6, 2]
   2. Multiplying a vector by a scalar, means multiplying each of its componenets by a that scalar.

Importance of Vector Addition and Multiplication

Later on we will see the importance of vector addition and multiplication. Ultimately no one view is right, what matters more is being able to utilize a specific view to understand the concept behind vectors.

Image:

I promise my illustration will get better :)