Three-Dimensional Linear Transformation

Significance of Two-Dimensions

Throughout most of the series now, we have worked primarily in two-dimensions. The reason being that most concepts are easier to grasp and understand fundamental in two-dimensional space. Once we understand the concepts, it is easier to translate them to higher dimensions.

Three-Dimensional Transformation

Let’s consider a linear transformation with three-dimensional vectors as inputs and three-dimensional vectors as outputs.

 [ 2 ]   L(v)   [ 3 ]
 [ 6 ]          [ 2 ]   
 [-1 ]          [ 0 ]   

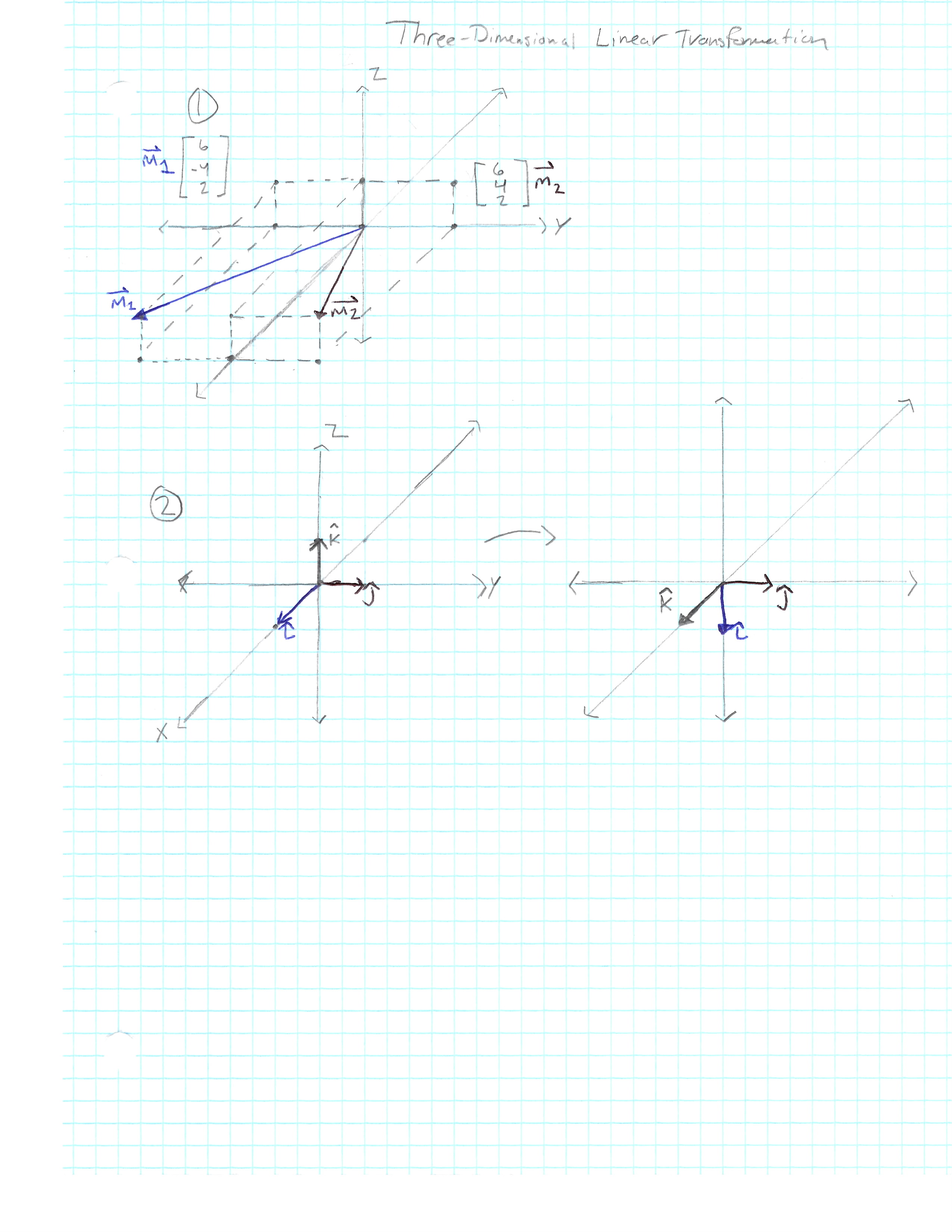
We can visualize this as a three-dimensional grid, which keeps the gridlines parallel, and evenly spaced, while also fixing the origin. Just as in two-dimensional space, every point we see moving is really just a proxy. A proxy for the vector who has it’s tip on that point.

What we are really visualizing is input vectors moving over to their corresponding outputs (See Picture 1). And just like with two-dimensions, what describes the transformation, is the output of the basis vectors. But now we have three basis vectors instead of two:

The unit vector in the x direction, i.

The unit vector in the y direction, j.

The unit vector in the z direction, k.

It’s easier to think of the transformations by following the basis vectors, since following the three-dimensional grid can get tricky.

i -> [ 1 ]   and   j -> [ 1 ]   and    k -> [ 1 ]
     [ 0 ]              [ 1 ]               [ 0 ]
     [ 1 ]              [ 0 ]               [ 1 ]

We can then take the coordinates of each basis vector,to give us the
matrix which completely describes the transformation.

[ 1  1  1 ]
[ 0  1  0 ]
[ 1  0  1 ]

Example

Let us consider a 90-degree rotation around the y-axis. The resulting coordinates for i and k would change, but not for j.

i    [ 1 ]       [ 0 ]
     [ 0 ]  -->  [ 0 ]
     [ 0 ]       [-1 ]

j    [ 0 ]       [ 0 ]
     [ 1 ]  -->  [ 1 ]
     [ 0 ]       [ 0 ]

k    [ 0 ]       [ 1 ]
     [ 0 ]  -->  [ 0 ]
     [ 1 ]       [ 0 ]

Those three sets of coordinates describe the columns of a matrix that describes the rotation transformation. (See Picture 2)

[ 1  0  0 ]      [ 0  0  1 ]
[ 0  1  0 ]  ->  [ 0  1  0 ]
[ 0  0  1 ]      [-1  0  0 ]

Coordinates of Output Vector

To see where a three dimensional input vector lands, the reasoning is almost identical for two dimensions. Each coordinate of the basis vectors can be thought as instructions for how to scale the input vector.

      [ x ]    
v  =  [ y ]  = xi + yj + zk
      [ z ]   

          input vector
             ˅   
[ 0  1  2 ][ x ]      [ 0 ]    [ 1 ]   [ 2 ]
[ 3  4  5 ][ y ]  =  x[ 3 ] + y[ 4 ] +z[ 5 ]
[ 6  7  8 ][ z ]      [ 6 ]    [ 7 ]   [ 8 ]
  ^  ^  ^               ^        ^       ^
Transformation                Output Vector

Composition of Two Transformations

Multiplying Matrices is done in the same manner as well. First, imagine the transformation done by the right matrix, then the transformation is done by the left matrix.

Three-dimensional matrix multiplication is actually very important for fields like computer graphics and robotics. Since concepts like complex rotation can be fairly hard to describe. But if you break them down into a composition of multiple rotations, the concept can be easier to understand.

Second Transformation
  ˅  ˅  ˅
[ 0 -2  2 ][ 0  1  2 ]
[ 5  1  5 ][ 3  4  5 ]
[ 1  4 -1 ][ 6  7  8 ]
             ^  ^  ^
            First Transformation

Once again, multiplication of three-dimensional matrices is similar to two-dimensional matrices. A good exercise is to reason through what this matrix multiplication should look like. Thinking closely about how it relates to the idea of applying two successive transformations in space.

If like me you can’t draw in three-dimensional space, take a look at this wonderful video